以前書いてたブログの記事をちょこちょこ直しつつこちらに引っ越しました。

最初に書いたのが2012年。全体的にネタが古い！

＊　　　＊　　　＊

コンピュータは2進法って話で面白かったのが、

片手で31まで数える方法、というやつです。

手でものを数えるときは、普通

といきますよね。

中学の頃友達と卓球で遊んだときは、

片手で片方のプレイヤーの得点を数えるために

5を超えたら手を裏返して

これで6

これが7

ということにしてました。

これでも中学生にとってはすげー発明だったわけですが、

コンピュータ関連の本を読んでいたら、

2進法の考え方を使うことで、31まで数える方法が紹介されていましたよ。

つまりこのように

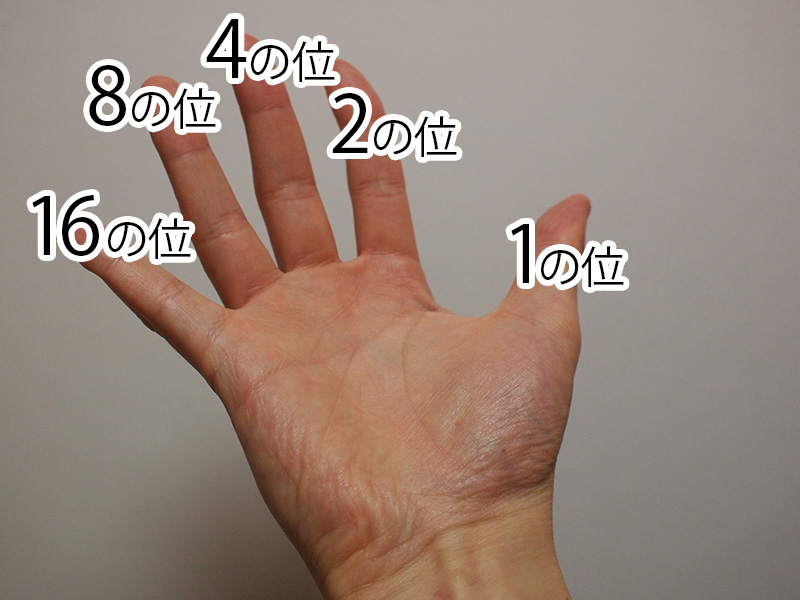
親指を1

人差し指を2

中指を4

薬指を8

小指を16

としてカウントしていくと…

親指は1。

人差し指は2。

人差し指2＋親指1＝3。

中指は4。

中指4＋親指1＝5。

中指4＋人差し指2＝6。

中指4＋人差し指2＋親指1＝7。

というふうにカウントアップできるわけです。

11。グワシっ

19。ゆーめをーかいたテストのーうーらー♪

31。これが2進法の限界。

…限界？

本当に限界？

中学の頃のあのワザが使えるんじゃないか？！

31を超えたってことを、手を裏返すことで表したらいいんじゃないか。

つまり。

これで32。ってことにしたらいけるじゃないか！

裏返す（32）＋親指（1）＝33。

裏返す（32）＋人指し指（2）＝34。

裏返す（32）＋人指し指（2）＋親指（1）＝35。

これなら63までいける！！

…でも、もしかしたらまだ方法があるんじゃないか。

まだやれる。

まだ俺、いける…！

つまり。

左向き（64）＋親指（1）＝65。

おわかりいただけただろうか…

手の向きで数字を表現してみました。

はい、だんだん数字に見えてきましたね？

左向き（64）＋裏返し（32）＋親指（1）＝97。

下向き（128）＋親指（1）＝129。

下向き（128）＋裏返し（32）＋親指（1）＝161。

右向き（192）＋裏返し（32）＋親指（1）＝225。

お逝きなさい！

はい、もう完全に数字ですね。

前向きを256とすると、

裏返しなど組み合わせて片手で319までいける計算です。

さて、これまでは片手でしたが

両手を組み合わせるともっと大きい数字もカウントできます。

左手の1を320とすることで、

102,399までカウントできますね。

たとえば。

アロハ！

スペシウム光線

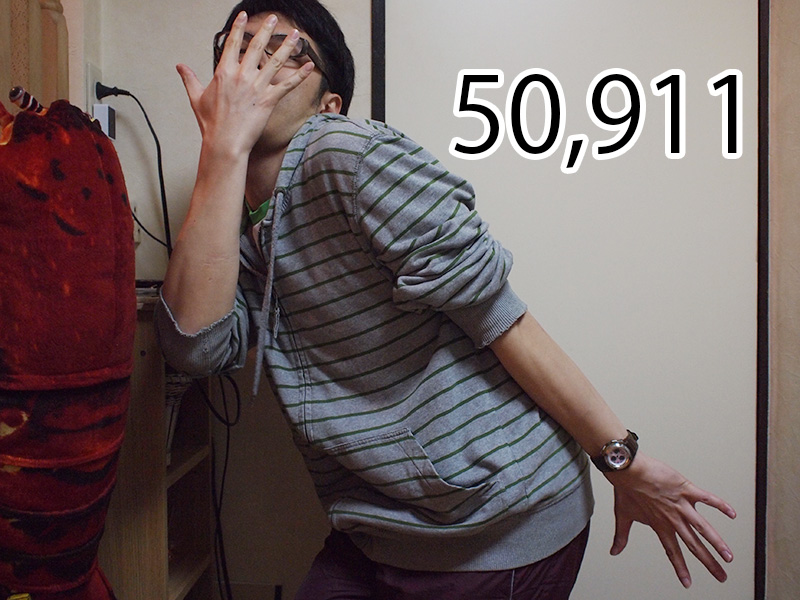
意外！それは髪の毛ッ！

いなかっぺ大将

ヴァンガードファイトしようぜ！

はい、これを利用すればいろいろなものの数が数えられますね！

みなさんも10万個程度のものなら両手で数えてみてください☆